Surface
tension
Surface tension is one of the everyday phenomena, like diffusion, which
one handles intuitively. One need not think
about it unless one wants to understand particular structures, as in
cherts
and fossils, brought about by the action of surface tension during
silicification.
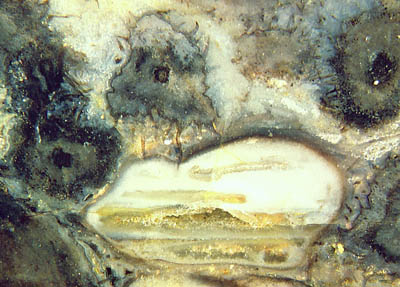
Fig.1: Swamp gas bubble squeezed between Trichopherophyton,
the bristly plant in the Lower Devonian Rhynie chert, lying prostrate
in the swamp. A
pointed bristle is
seen piercing the surface of the bubble. Apparently both the bubble and
the bristle are
deformed thereby: not important but instructive.
The deformation of the bristle may be due to
lengthwise compression as a reaction of the deformed liquid surface
and thus serve as fossil evidence for an effect of surface tension
other than shaping liquid surfaces.
Contrary to an occasionally upheld view, horizontal bands
like the one
inside the bubble do not
indicate the presence of a water level during silicification. The
effects of surface tension are commonly known: It tends to shape
liquid
droplets, soap bubbles, and bubbles within a liquid into spheres.
However,
the term is not self-explanatory and often misunderstood, even by
physicists. What surface tension means can be
illustrated by a thought experiment which could be performed in reality
as well.
Imagine a square frame made of thin wire with a thin
sheet of soap water suspended within. (Why soap water is much more
suitable than plain water for this purpose would be difficult to
explain and is not relevant here. A suspended liquid sheet is easily
obtained by dipping the frame in.) The tension of the sheet reveals
its presence and its magnitude by pulling the sides of the frame inward
or even crushing the frame into a tangle of wire if the wire is very
thin.
The magnitude of the pull can be measured by applying a force pulling
the sides of the frame outward until they are straight again. It is
found that the required force is proportional to the side length of the
frame, hence the tension of the liquid sheet is
reasonably quantified as force per length.
Since the liquid sheet has two surfaces, the surface tension of the
liquid itself is half the measured tension of the sheet.
The logic is not yet complete here: It has to be shown that the pull is
exerted by the surface layers alone but not also by the
variable amount of water trapped in between. It is found
that the pull of the sheet is independent of the amount of trapped
liquid, hence it is really a surface effect. (So it becomes obvious
that it would not be useful to quantify surface tension as a tensile
stress in the usual sense, which would be force per area of sheet
cross-section.)
Another important
property of liquid surfaces has been tacity assumed in the above
thought experiment: Unlike elastic sheets, whose tension would rise if
extended and decrease to zero if left to relax, liquid surfaces retain
their tension independent of any change of the area. This
means a liquid surface always retains its tendency to reduce its area
as much as possible, which makes spherical drops and bubbles if there
is no hindrance to taking spherical shapes. In other words:
When the air is left out of a balloon, the tension of the rubber
relaxes to zero. When
the air is slowly left out of a soap bubble through a straw, the
surface
tension remains the same, (which implies that the pressure inside
even increases, as required by the equilibrium of forces).
Although the shapes of liquid surfaces can be
understood with the notion of surface tension as force per length of
surface boundary as proposed above, it is worth mentioning that force
per length is equivalent to energy per area in this case. This surface
energy is stored in the molecules lying at the surface and thus being
less
tightly bound to their surroundings than the molecules inside. The
energy was put in when the surface was created, and it is available for
moving things like pulling the liquid into
equilibrium shape or bending the frame. Since the energy per surface
area can
reasonably be assumed to be a property of the liquid and hence
independent of the area, it is obvious that its equivalent,
the surface tension, is also independent of the area.
The phenomenon of
wetting, which is of great practical relevance, is only briefly
mentioned here. The physics of wetting can be understood by extending
the concept of surface
tension to solids and to interfaces between liquids and solids, where
the notion of "energy per area" is useful again since "force
per length" could not be measured as with liquid surfaces. A
combination of the three material properties makes the contact angle, a
quantity which can easily be measured. Zero contact angle, as observed
with soap water on many solid surfaces, means perfect wetting (which is
the very purpose of applying soap). Ideal
non-wetting with 180° contact angle can be approached with specially
prepared anti-wetting surfaces.
It depends on the contact angle how far
a liquid is drawn up or down in a narrow tube also called
capillary, hence the term capillary force for surface tension. (There
is a repeatedly told
myth that water is drawn into the tree tops by capillary force.
Sometimes there are attempts to overcome the inconsistencies inherent
in this hypothesis by elaborate constructs. Why such attempts are in
vain will be explained elsewhere on this website.)
As one of the most common manifestations of surface tension, small
wettable things tend to stick together when wet. Less obvious because
seldom observed is another effect: Bubbles trapped under water push
wettable things aside as they grow, as by accumulating swamp gas, for
example. (They would pull non-wettable things inside.)
Occasionally
it is found that the
arrangement of plant parts preserved in chert had been influenced by
these manifestations of surface tension. During the earliest stages of
silicification, swamp gas bubbles can become trapped in the soft silica
gel between the plants.
Plant parts can be displaced by the bubbles and fixed in that position.
Later, as the gas vanishes by diffusion,
the bubbles become
filled with water and finally also turn into gel and chalcedony so that
the cause of the displacement is not immediately obvious.
Fig.2: Rhynia
shoots being pushed by swamp gas bubbles below and above,
without particular effect in this case. After
the cavities had become filled with
water, aquatic fungus hyphae grew there before all turned into
silica gel and finally into chalcedony.
The capillary force is a dangerous force of nature for small
creatures. Small
creatures
need not be careful not to stumble and fall but they must be carefully
avoid getting wet lest they be trapped by a drop of water.
What is
meant by "small" in this connection becomes obvious by looking at water
spilled on a table: Small drops come close to a spherical cap,
large drops are flat on the top, and none is higher than about 4mm. (A
related graphic at Wikipedia is not helpful as it compares 3 drops
differing in both volume and contact angle, and the flat top of big
drops is not indicated.) This height of about 4mm is a suitable measure
for a rough distinction between "small" and "big" in connection with
surface tension effects of water.
As one plausible but not immediately obvious
implication, water cannot form a level in a "small" cavity since its
surface is necessarily curved in situations where the pull of surface
tension outweighs gravity. Hence,
level
bands (really level planes) in the chalcedony fill of small
cavities cannot have formed at water levels. The horizontal
planes had formed in connection with the plane surface of settled
suspensions of silica clusters in water-filled cavities.
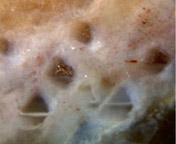
Fig.3: Level bands in hollow conifer needles had not been water levels.
The surface tension of water in half-filled cavities
as small as these would force the air into a spherical bubble. Lower
Permian chert, Döhlen basin, Germany.
Small creatures have developed intricate means of keeping
dry, usually
a waxy coating making a water contact angle well above 90°, combined
with a
surface structure with closely spaced small mounds, ridges, bristles,
hairs, etc., where the liquid contacts only the tips. This makes an
average interface energy which can be much
smaller than the local one, which results in an effective contact angle
much larger than the local one, which means an anti-wetting
effect much better than that of the plain surface.
As for spiders and their kin, proper handling of liquids
is one of the most important skills. They must be able to handle drops
of sticky liquid without soiling themselves when eating. This
gives rise to the suspicion that some or
even most of the arrays of projections and hairs seen on the mouth
parts of some
arthropods [1], usually regarded as filtering devices, might be no
such.
They might well be efficient means of handling liquid drops and keeping
them
away from the body parts.
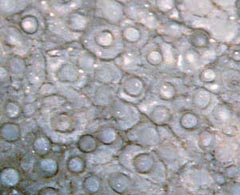
Filamentous plants, as pond algae
looking like fluffy cotton wool, would be completely flattened when
taken out of the water. Nematophytes, the "filamentous
plants" now
listed among "Enigmatic Organisms" [2], seem to have invented a
particular way of avoiding being crushed by surface tension when their
habitat temporarily falls dry: living within a lump of organic gel.
Fig.4: Nematophyte: filaments in gel, apparently as a protection
against both
exsiccation and collapse when out of the water.
Rhynie chert, Lower Devonian.
H.-J.
Weiss
2013
[1]
J.A. Dunlop, S.R. Fayers, H. Hass, H. Kerp: A
new arthropod from the early Devonian Rhynie chert, Aberdeenshire
(Scotland),
with a
remarkable filtering device in the mouthparts. Paläontol. Z. 80(2006),
296-306.
[2] T.N.
Taylor, E.L. Taylor, M. Krings:
Paleobotany,
Elsevier 2009.